
Also be on the lookout for multiples like 10-24-26 and 2.5-6-6.5. The second Pythagorean triple that commonly appears on tests is 5-12-13 (5 2 + 12 2 = 13 2, 25 + 144 = 169). In this formula, Area of Isosceles Right Triangle uses Perimeter of Isosceles Right Triangle.Since the short legs of an isosceles triangle are the same length, we need to. The same holds true for 9-12-15, and even 1.5-2-2.5. To find the area of a triangle, multiply the base by the height, then divide by 2. For example a right triangle with legs of length 6 and 8 will have a hypotenuse of 10 (6 2 + 8 2 = 10 2, 36 + 64 = 100). The ratio of a Pythagorean triple holds true even when the sides are multiplied by another number.
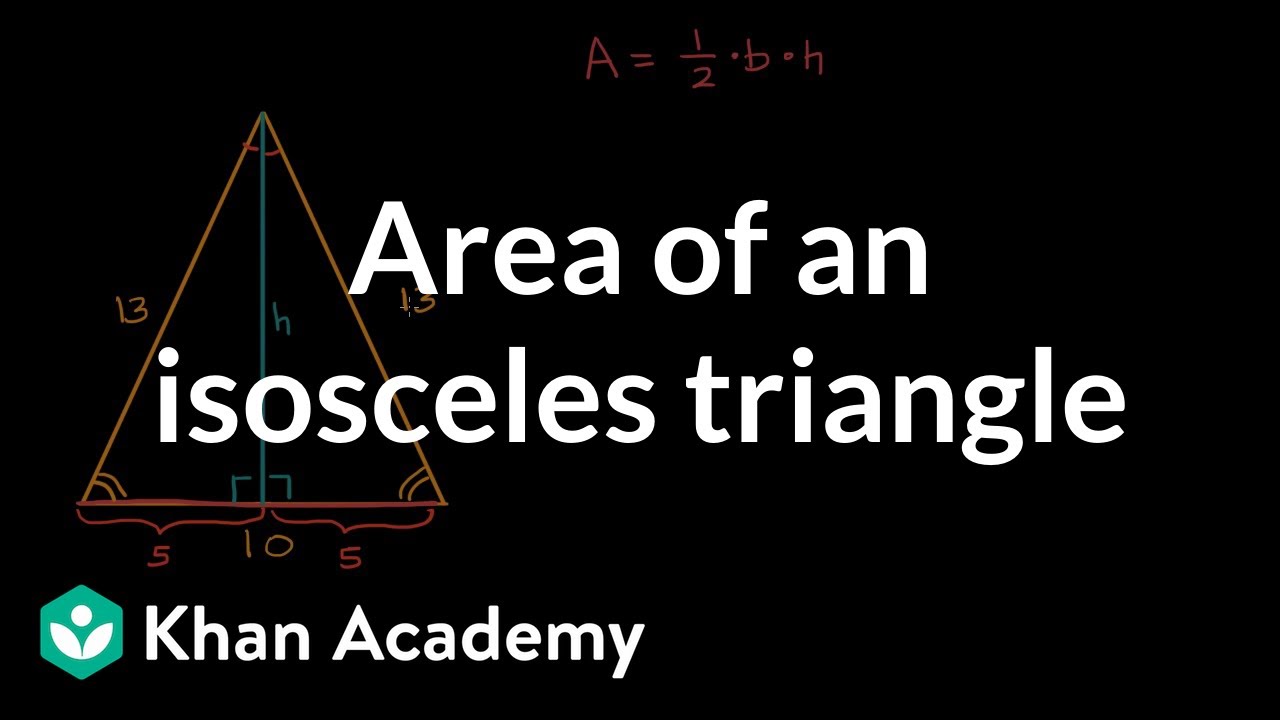
When you see a right triangle with legs of length 3 and 4, you can instantly be certain that the hypotenuse will be 5 without having to do any calculations. In our tree problem, our two sides are the 10 feet and the 30 feet the. If you memorize the first 2 Pythagorean triples, in particular, you can save yourself a lot of time on these tests because you can immediately know the hypotenuse of one of these triangles just by looking at the side lengths! X Research source In formula form, it is a2 + b2 c2, where a and b are the two sides of the right triangle and c is the hypotenuse. Solution: The two equal sides of the isosceles right triangle are the base and perpendicular. These special triangles appear frequently in geometry text books and on standardized tests like the SAT and the GRE. For an isosceles right-angled triangle, the two smallest sides are equal to 10cm. The side lengths of a Pythagorean triple are integers that fit the Pythagorean Theorem. However, any Pythagorean triangle with legs x, y and hypotenuse z can generate a Pythagorean triangle with an integer altitude, by scaling up the sides by the length of the hypotenuse z.Learn to recognize Pythagorean Triple Triangles. This is the integer closest to p 2 / 48 is in fully reduced form since c cannot equal 1 for any primitive Pythagorean triangle, d cannot be an integer.
So the number of integer triangles (up to congruence) with perimeter p is the number of partitions of p into three positive parts that satisfy the triangle inequality.

) Therefore the three sides are in the ratio. To find the ratio number of the hypotenuse h, we have, according to the Pythagorean theorem, h2 1 2 + 1 2 2. Each such triple defines an integer triangle that is unique up to congruence. In an isosceles right triangle, the equal sides make the right angle. General properties for an integer triangle Integer triangles with given perimeter Īny triple of positive integers can serve as the side lengths of an integer triangle as long as it satisfies the triangle inequality: the longest side is shorter than the sum of the other two sides. Sometimes other definitions of the term rational triangle are used: Carmichael (1914) and Dickson (1920) use the term to mean a Heronian triangle (a triangle with integral or rational side lengths and area) Conway and Guy (1996) define a rational triangle as one with rational sides and rational angles measured in degrees-the only such triangles are rational-sided equilateral triangles. A rational triangle is one whose side lengths are rational numbers any rational triangle can be rescaled by the lowest common denominator of the sides to obtain a similar integer triangle, so there is a close relationship between integer triangles and rational triangles. A Heronian triangle with sidelengths c, e and b + d, and height a, all integers.Īn integer triangle or integral triangle is a triangle all of whose side lengths are integers.


 0 kommentar(er)
0 kommentar(er)
